Inclusive Jet Cross Sections in DIS
Nowadays more or less everybody knows about the concept of electric charge. Charge comes as positive or negative, and like-sign charges repel each other whilst opposite-sign charges feel an attractive force towards each other. Electric charge can be considered as a property of an object, for example an elementary particle. Perhaps the simplest and best-known electrically charged fundamental particle is the electron - where `fundamental' means point-like according to our current knowledge.

Some decades ago, however, the idea evolved that there might be other properties of particles which merit the name `charge' because these properties also give rise to attractive or repulsive forces. One of these properties was labelled `color charge' or simply `color' and comes in three kinds which are named `red', `blue' and `green'. Just as the theory of electromagnetism describes the behaviour of electrically charged particles, a theory called Quantum Chromodynamics (QCD) was developed, which describes the dynamics of colored objects.

As far as we know today, there are basically two kinds of color-charged elementary objects, which we call quarks and gluons. The quarks were once suggested as a purely theoretical concept, but later turned out to be the basic building blocks of all complex particles and, therefore, of the macroscopic world around us. The gluons, according to QCD, bind the quarks together and thereby make possible the existence of complex particles such as the proton. The proton is now known to be built from three `valence' quarks with colors red, blue and green, resulting in an overall `white' or color-neutral object. QCD governs the way in which the valence quarks interact with one another.

QCD is much richer and more complex than the theory of the electromagnetic force. One important difference is that colored objects are `confined' - only color-neutral objects can exist on their own. This is why we were never able to observe isolated quarks or gluons - in contrast to electrons. So if one wants to investigate QCD, one somehow has to look inside composite particles like the proton and study the behaviour of the quark and gluon building blocks. This is one of the reasons for the construction of the HERA accelerator which collides, at very high energies, protons with electrons. The electron acts as a probe that explores the structure and the dynamics within the proton.

In the high energy electron-proton interactions at HERA, the electron can scatter violently from an electrically charged component of the proton, i.e. a quark, but not a gluon. The quark can be kicked out of the proton and can be observed as a collimated spray of particles (a jet) hitting the H1 detector (remember that quarks cannot be seen in isolation, so the struck quark drags accompagnying particles litterally from nowhere - from the vacuum - in order to neutralise its colour). Alternatively, a gluon inside the proton can split into a quark-antiquark pair, allowing the electron to couple to one of those two. In this case, two jets might be observed, one from each of the two quarks into which the gluon splits. There are even more possibilities, since both quarks and gluons are also able to radiate gluons, which may also split into even more quarks and gluons, ultimately producing a `cascade' of particles between the struck quark and the remnants of the proton. All of the particles of the cascade might emerge as jets. A typical electron proton collision thus results in very complex distributions of jets and particles in the detector. One of the central aims of the HERA experiments is to obtain a deeper understanding of the QCD dynamics involved in producing these complex patterns of particle activity emerging from the interactions. In this publication, we aim to improve this understanding by studying the distributions of the produced jets in terms of their energy transverse to the beam direction (ET) and the angles at which they are produced, parameterised by the `pseudorapidity' (etalab).

Since QCD is a very complicated theory, predictions can only be made using approximations. It is interesting and important to ask how valid these approximations are in as many different experimental situations as possible. The most successful approximation that we have at present for the descripion of colour dynamics is known as next-to-leading order (NLO) DGLAP. In this analysis, the predictive power of this approximation is tested in detail through comparisons with the measured jets from data collected with the H1 detector in the years 1996 and 1997.

One of the results of the analysis is shown in the plot below. In the upper part of the figure we plotted as black points the probability (in some complex notation) of finding a jet with a a certain ET. These data points are compared to a solid line with a yellow band around it. The line shows the NLO DGLAP theoretical predictions, and the yellow band is the uncertainty in this prediction. The dashed line shows the predictions of a less sophisticated approximation, leading order (LO) DGLAP. In order to look more closely for discrepancies, the bottom part of the figures shows the relative difference beteen the NLO DGLAP theory and the measured data. The analysis is done in three different regions of the detector - from left to right, close to the direction of the outgoing electron beam, in the middle of the detector, and close to the direction of the outgoing proton beam.

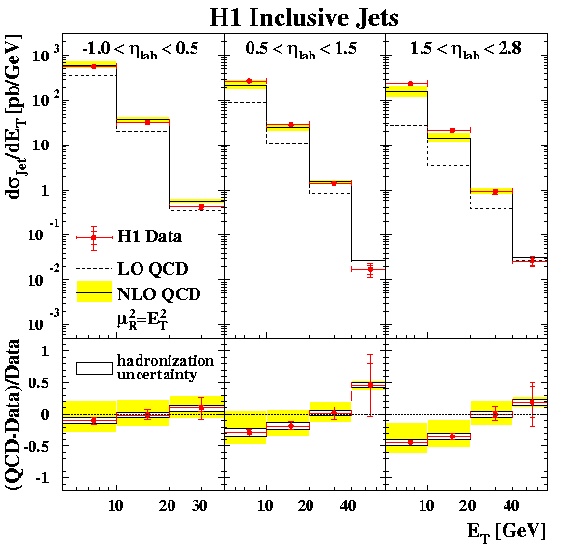
Fig 1 of paper

A close look at the figure shows that for jets produced in the central and outgoing electron directions, the agreement between the data and the theoretical predictions is impressive, thus increasing our confidence in the predictive power of the theory in these experimental regions. However, there is a clear discrepancy between the data points and the yellow band in the right column of the figure, corresponding to jets produced near to the remnants of the proton. This last region is expected to be the most difficult to describe and interesting, because it is furthest from the interaction between the electron and the final struck quark. It is thus the most sensitive to the details of the cascade of quarks and gluons mentioned above. A variety of novel QCD effects have been predicted for this region. However, the discrepancies between data and theory near to the proton remnant are only present for low values of the variable ET, where NLO DGLAP is known to be less complete than at higher values. Just look at the difference between the LO and NLO predictions in the upper right part of the plot. The most likely explanation seems to be that a still more precise version of the theory is needed, for example an extension of one more order to next-to-next-to-leading order (NNLO DGLAP).

What did we learn from this analysis? Firstly we confirmed the applicability of the best approximation to QCD that we have to date (NLO DGLAP) for the description of jets in a wide variety of circumstances. Secondly, it is clear that our result should trigger additional effort in developing more complete theoretical predictions. Only time will tell whether a refinement of DGLAP to NNLO will be able to resolve the differences near to the proton remnants or whether a whole new approach, not based on the DGLAP approximation, will be required. This analysis is one of the many small building blocks which together give us a detailed picture of the microscopic world and help us to understand better and ever better the world we are living in.